[프로그래머스] 카카오 - 합승 택시 요금

문제

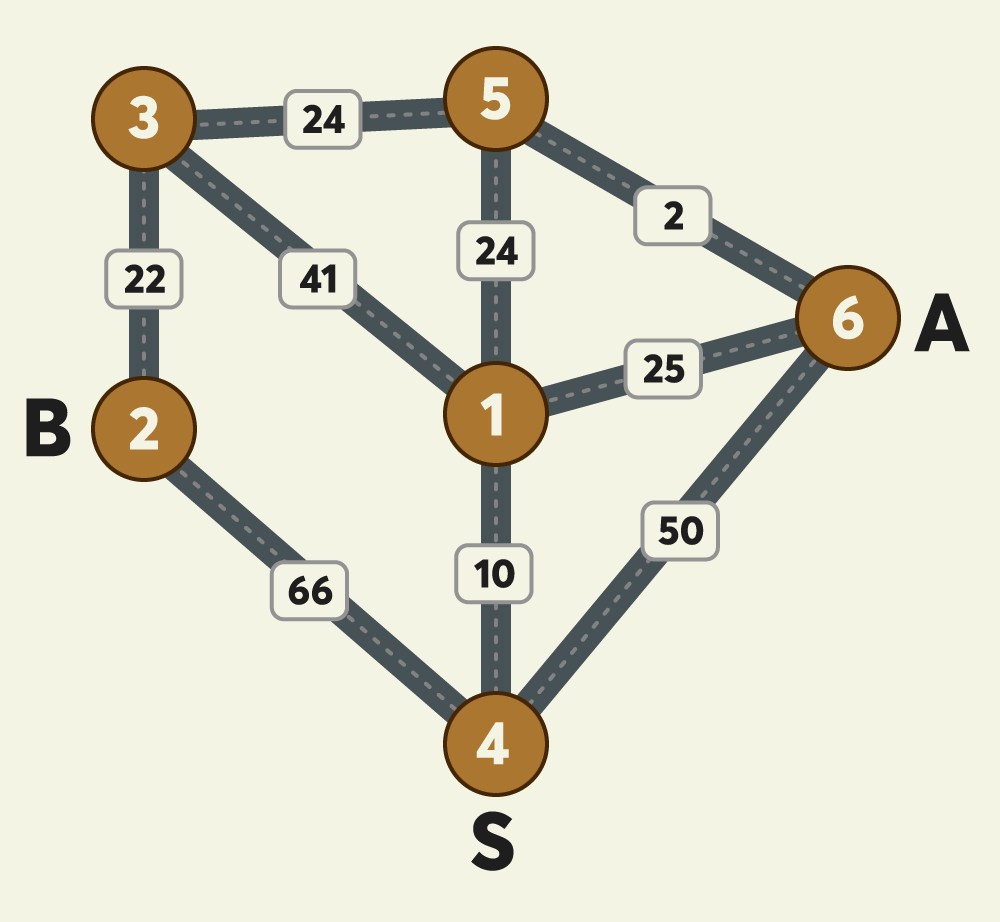
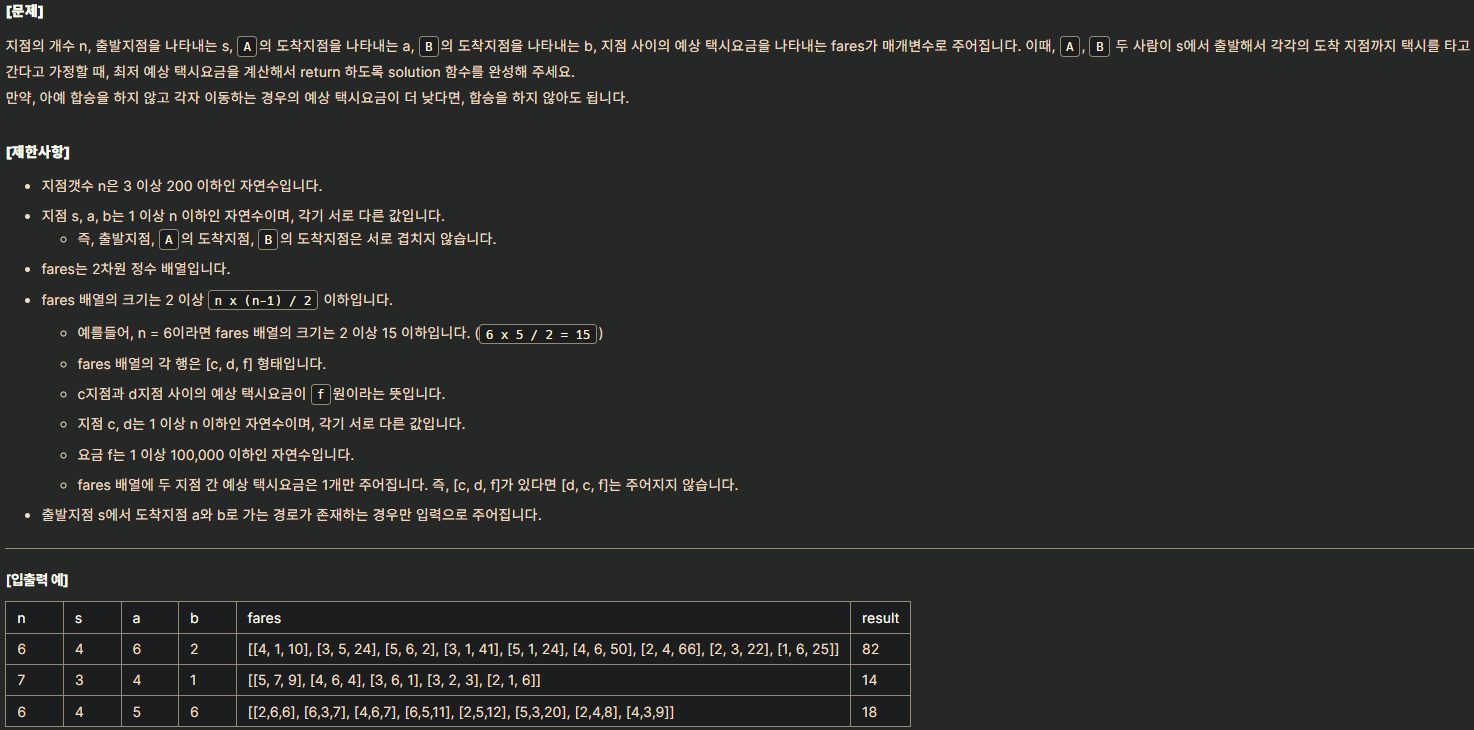
2021 카카오 블라인드 채용 - 합승 택시 요금

https://school.programmers.co.kr/learn/courses/30/lessons/72413

 

 

풀이

설명

A, B 두 사람이 s에서 출발해서 각각의 도착 지점까지 택시를 타고 간다고 할 때, 최저 예상 택시 요금을 구하는 문제입니다.

 

A, B 둘이서 임의의 지점 x까지 합승해서 간다고 할 때, 최저 택시 요금은 다음과 같습니다.

s에서 x까지의 택시요금 + x에서 a까지의 택시 요금 + x에서 b까지의 택시 요금

 

s, a, b 각각에서 그래프 탐색을 통해 각 노드까지의 최소 요금을 구합니다.

모든 노드를 순회하며 s, a, b에서 해당 노드까지의 요금을 구하고, 최소 요금을 업데이트합니다.

 

예시 코드

class PriorityQueue {
  constructor() {
    this.heap = [];
  }

  enqueue(value, priority) {
    this.heap.push({ value, priority });
    this.heapUp();
  }

  dequeue() {
    if (this.size() === 0) return null;
    if (this.size() === 1) return this.heap.pop();

    const min = this.heap[0];
    this.heap[0] = this.heap.pop();
    this.heapDown();

    return min;
  }

  heapUp() {
    let child = this.size() - 1;

    while (child > 0) {
      const parent = this.getParent(child);
      if (this.heap[child].priority >= this.heap[parent].priority) break;

      this.swap(child, parent);
      child = parent;
    }
  }

  heapDown() {
    let parent = 0;

    while (true) {
      const left = this.getLeftChild(parent);
      const right = this.getRightChild(parent);
      let smallest = parent;

      if (
        this.isValidChild(left) &&
        this.heap[left].priority < this.heap[smallest].priority
      )
        smallest = left;

      if (
        this.isValidChild(right) &&
        this.heap[right].priority < this.heap[smallest].priority
      )
        smallest = right;

      if (smallest === parent) break;

      this.swap(parent, smallest);
      parent = smallest;
    }
  }

  swap(a, b) {
    [this.heap[a], this.heap[b]] = [this.heap[b], this.heap[a]];
  }

  size() {
    return this.heap.length;
  }

  isEmpty() {
    return this.size() === 0;
  }

  getParent(child) {
    return Math.floor((child - 1) / 2);
  }
  getLeftChild(parent) {
    return parent * 2 + 1;
  }
  getRightChild(parent) {
    return parent * 2 + 2;
  }
  isValidChild(index) {
    return index < this.size();
  }
}

function solution(n, s, a, b, fares) {
  const graph = Array.from({ length: n + 1 }, () => []);

  for (const [u, v, w] of fares) {
    graph[u].push([v, w]);
    graph[v].push([u, w]);
  }

  const distFromS = dijkstra(s);
  const distFromA = dijkstra(a);
  const distFromB = dijkstra(b);

  let minFare = Infinity;
  for (let i = 1; i <= n; i++) {
    const fare = distFromS[i] + distFromA[i] + distFromB[i];
    minFare = Math.min(minFare, fare);
  }

  return minFare;

  function dijkstra(start) {
    const dist = Array(n + 1).fill(Infinity);
    const pq = new PriorityQueue();
    pq.enqueue(start, 0);
    dist[start] = 0;

    while (!pq.isEmpty()) {
      const { value: node, priority: cost } = pq.dequeue();

      for (const [next, weight] of graph[node]) {
        const newCost = cost + weight;
        if (newCost >= dist[next]) continue;

        dist[next] = newCost;
        pq.enqueue(next, newCost);
      }
    }

    return dist;
  }
}